Dichtungen sind allgemeine Strukturbauteile, die oft Konstruktionsanalysen erfordern. Abaqus kann nichtlineare Finite-Elemente-Analysen von Dichtungen durchführen und die Dichtungsleistung überprüfen.
In diesen Analysen lassen sich Dichtungsverformungen und -spannungen sowie eine Kontaktdruckverteilung bestimmen. Abaqus ermöglicht die Berücksichtigung von Pressure-Penetration-Effekten zwischen der Dichtung und den Kontaktflächen in diesen Analysen, wodurch Analysen von Dichtungen realistischer und genauer werden.
Diese Funktion simuliert das Flüssigkeitseindringen bzw. die Druckdurchdringung zwischen sich berührenden Oberflächen. Es wird durch die Verwendung der Druckpenetrationsoption aufgerufen. Dieser Luftdruck dringt in die Fuge ein und belastet die die Fuge bildenden Oberflächen, bis ein Bereich der Oberflächen erreicht wird, in dem der Kontaktdruck zwischen den aneinanderstoßenden Oberflächen den kritischen Wert überschreitet, der in der Druckpenetrationsoption angegeben ist, wodurch ein weiteres Eindringen verhindert wird.
In diesem Blog wird ein konkretes Beispiel von Abaqus berechnet, um Pressure-Penetration zu präsentieren.
Finite-Elemente-Modell
Geometrie
Die betrachtete Baugruppe lässt sich mit einem 3D-Modell abbilden. Es besteht aus 2 Teilen, einer Gummidichtung in Grün und einem Stahlrohr in Weiß. Beide Bauteile sind mithilfe der symmetrischen Lagerbedingung modelliert und an einem oder mehreren Enden durch den Flüssigkeits- oder Luftdruck belastet.
Dieser Druck dringt in die Gummidichtung ein, bis ein Bereich der Oberflächen erreicht wird, in dem der Kontaktdruck zwischen den aneinanderstoßenden Oberflächen den kritischen Wert überschreitet. Dadurch wird ein weiteres Eindringen verhindert.
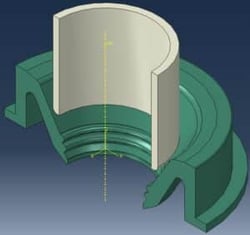
Abbildung 1: Geometrie der Gummidichtung und des Stahlrohrs in Abaqus/CAE
Modellierung des Problems
Materialeigenschaften
Die Gummidichtung wird mit einem einfachen Neo Hooke Material Modell (Hyperplastisch) mit den Parametern C10 = 0.752 und D1 = 0.026 modelliert.
Das Stahlrohr wird als starrer Körper modelliert, indem eine Starrkörper-Einschränkung angewendet wird.
Vernetzung
Die Gummidichtung und die Stahlstange sind mit Hex-Elementen vernetzt. Der zugewiesene Elementtyp sind C3D8R in Abaqus/Standard-Berechnungen.

Abbildung 2: Vernetzung von Gummidichtung und Stahlstange in Abaqus/CAE
Kontakteigenschaften
Die Kontakteigenschaften sind wie folgt:
- das tangentiale Verhalten – 0.1 als Reibungskoeffizient
- das normale Verhalten – Hardkontakt
Analyse-Schritte
Die ausgeschnittene Fläche der Gummidichtung wird während der gesamten Simulation in der Z-Richtung symmetrisch fixiert. Zudem wird die Außenfläche der Dichtung fest gelagert.
Der Stahlstange wird um 10 mm nach unten bewegt, um in die Gummidichtung in Schritt 1 zu stecken.
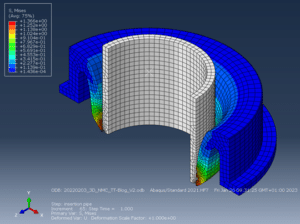
Abbildung 3: Verformte Form nach Schritt 1
Schritt 2 simuliert die Auswirkungen von unter Druck stehendem Fluid, das von oben in den modellierten Bereich eintritt und Druck auf den freiliegenden Teil der Gummidichtung ausübt.

Abbildung 4: Verformte Form nach Schritt 2
In Schritt 3 wird das Stahlrohr in der horizontalen Richtung um 3mm verschoben. Damit lässt sich die Fluiddruck wegen der Veränderung der Kontaktbedingungen teilweise absperren und teilweise freischalten.
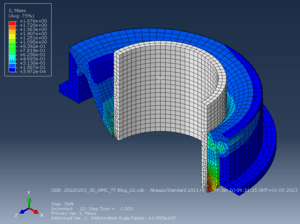
Abbildung 5: Verformte Form nach Schritt 3
Definieren der Pressure-Penetration-Interaktion
Der Kontaktpaar-Ansatz wird verwendet, um den Kontakt zu modellieren, wo die Druckdurchdringung wahrscheinlich auftritt.
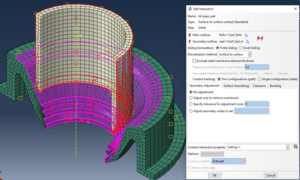
Abbildung 6: Kontaktpaar
Anschließend kann die zuvor definierte Kontaktinteraktion ausgewählt werden, sodass die Main- und Secondary-Oberfläche bereits bekannt ist. Sowohl auf der Main- als auch auf der Secondary-Oberfläche ist ein Bereich zu definieren, in dem der Druck anfänglich angewendet wird. Hierbei ist der Bereich auf der Secondary-Oberfläche pflichtig.
In diesem Fall werden die in Abb. 7 durch Pfeile angezeigten Bereiche ausgewählt. Der Druck dringt dann automatisch bis zum ersten Dichtungszahn ein.
Außerdem muss ein Fluiddruck angegeben werden. Das ist der Druck, der im nicht kontaktierenden Bereich aufgebracht wird. In diesem Fall wird ein Flüssigkeitsdruck von 0.05 MPa gewählt, der während des Simulationsschritts hochgefahren wird.
„Critical Contact Pressure“ bestimmt den kritischen Wert des Kontaktdrucks zwischen den aneinanderstoßenden Oberflächen, wodurch ein weiteres Eindringen verhindert wird.
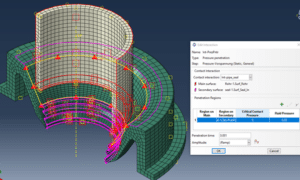
Abbildung 7: Pressure-Penetration-Interaktion
Schließlich wird ein Selbstkontakt der Gummidichtung zugeordnet.
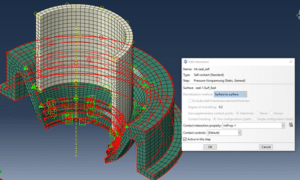
Abbildung 8: Selbstkontakt-Interaktion
Die Feldausgabe PRESS wird angefordert. Dies ist der Druck, der aufgrund der Druckdurchdringung auf die Oberfläche ausgeübt wird. Dies zeigt, wo der Druck ausgeübt wird, sowie seine aktuelle Größe.
Ergebnisse
Wie Abb. 9 darstellt, lässt sich der Fluiddruck durch den Kontakt stoppen.
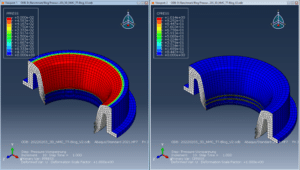
Abbildung 9: PPRESS nach Schritt 2
Nach der seitlichen Verschiebung des Rohrs wird der Kontakt des ersten Dichtungszahns auf der linken Seite getrennt. Das ermöglicht die Druckpenetration bis zum zweiten Zahn.
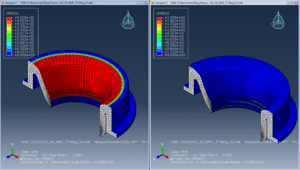
Abbildung 10: PPRESS nach Schritt 3




 Advanced Simulation
Advanced Simulation


 Engineering
Engineering